PyMieDiff + TorchGDM: Optimize a Huygens lens#

This example demonstrates how to design a diffractive lens made of core‑shell nanospheres by jointly optimizing their positions and geometrical parameters (core radius, shell thickness) with gradient‑based autodiff. The workflow is:

Define the optical environment (free‑space, illumination, material database for Si and Au).
Initialize a regular grid of scatterers and treat the (x, y) coordinates, core radii and shell thicknesses as differentiable parameters.
Build an autodiff‑compatible Mie scattering model using pymiediff –> torchgdm (StructAutodiffMieEffPola3D, assuming a purely dipolar response for computational speed).
Run a full‑wave simulation (torchgdm.Simulation) and compute the near‑field intensity at a user‑specified focal point.
Define a loss that maximizes the intensity at the focus while penalising overlapping particles. Minimise it iteratively with Adam (gradient based).

Notes#

requires torchgdm: wiechapeter/torchgdm
TorchGDM paper: S. Ponomareva et al. SciPost Physics Codebases 60 (2025) doi: 10.21468/SciPostPhysCodeb.60

author: P. Wiecha, 11/2025

imports#

import time
from dataclasses import dataclass

import matplotlib.pyplot as plt
import torch

import torchgdm as tg
import pymiediff as pmd

configuration#

configure illumination and materials for the Huygen’s type diffractive lens

# environment
n_env = 1.0
env = tg.env.freespace_3d.EnvHomogeneous3D(env_material=n_env**2)

# illumination (and wavelength)
wavelengths = torch.tensor([700.0])
e_inc_list = [tg.env.freespace_3d.PlaneWave(e0p=1.0, e0s=0.0, inc_angle=torch.pi)]

# core and shell materials
mat_si = pmd.materials.MatDatabase("Si")
mat_au = pmd.materials.MatDatabase("Au")

# geometry limits (core radius and shell thickness, in nm)
r_c_lim = [50, 130]
d_s_lim = [0, 30]


# optimizer config
@dataclass
class OptConfig:
    optimizer = torch.optim.Adam
    lr = 20.0  # note: learningrate is highly problem specific
    n_iters = 30
    dist_min = 400.0
    dist_weight = 1e-2
    device = "cpu"

setup the optimization#

# optimization target
z_focus = -6000
r_target = torch.as_tensor([[0, 0, z_focus]], device=OptConfig.device)

# initialize geometry: uniform grid
# Note: it's required to specify the device before setting `require_grad``
z0_metasurface = 0
D_area = 7000
N_particles = 10  # construct grid of N x N particles
geo_pos_init = tg.tools.geometry.coordinate_map_2d_square(
    D_area / 2, N_particles, z0_metasurface
)
geo_pos_init = geo_pos_init["r_probe"][:, :2]  # optimize x,y coordinates
geo_pos = geo_pos_init.clone().detach().to(OptConfig.device)
geo_pos.requires_grad = True

rc_init = torch.zeros(len(geo_pos_init), device=OptConfig.device)
geo_rc = rc_init.clone().detach()
geo_rc.requires_grad = True

rs_init = torch.zeros(len(geo_pos_init), device=OptConfig.device)
geo_rs = rs_init.clone().detach()
geo_rs.requires_grad = True

# init the optimizer with the target parameters
optimizer = OptConfig.optimizer([geo_pos, geo_rc, geo_rs], lr=OptConfig.lr)

define fitness function#

the goal will be to design a lens by positioning the scatterers on a plane. the fitness function therefore will calculate the field enhancement at a target position (the focus of the lens). The free parameters are the (x,y) coordinates of many identical nanostructures (using a list of their positions).

sigmoid = torch.nn.Sigmoid()


def _radii_from_params(core_param: torch.Tensor, shell_param: torch.Tensor):
    """
    Convert optimisation parameters (unbounded) into physically meaningful
    core‑ and shell‑radius values (nm) using the pre‑defined limits.
    """
    # apply limits through sigmoid (so internal optimization parameters go from 0 to 1)
    rad_core_nm = r_c_lim[0] + (r_c_lim[1] - r_c_lim[0]) * sigmoid(core_param / 200.0)
    rad_shell_nm = (
        rad_core_nm
        + d_s_lim[0]
        + (d_s_lim[1] - d_s_lim[0]) * sigmoid(shell_param / 200.0)
    )
    return rad_core_nm, rad_shell_nm


def func(r_pos, core_param, shell_param, r_target, env, e_inc_list, wavelength, z0=0):
    # --- create assembly of many same structures at `r_pos` positions
    r_pos = torch.concatenate((r_pos, z0 * torch.ones_like(r_pos)[:, :1]), dim=1)
    struct_list = None

    # --- convert optim params to physical radii
    rad_core_nm, rad_shell_nm = _radii_from_params(core_param, shell_param)

    # --- build autodiff‑compatible structure list for torchGDM
    for i in range(len(r_pos)):
        # create pymiediff particle
        mie_particle = pmd.Particle(
            r_core=rad_core_nm[i],
            r_shell=rad_shell_nm[i],
            mat_core=mat_si,
            mat_shell=mat_au,
            mat_env=n_env,
            device=r_pos.device,
        )

        # convert to auto-diff capable torchGDM structure
        _st = pmd.helper.tg.StructAutodiffMieEffPola3D(
            mie_particle=mie_particle,
            wavelengths=wavelength,
            verbose=False,
        )
        _st.set_center_of_mass(r_pos[i])

        if struct_list is None:
            struct_list = _st
        else:
            # inplace combining (inplace required for AD)
            struct_list = struct_list.combine(_st, inplace=True)

    # --- create and run simulation
    sim = tg.simulation.Simulation(
        structures=[struct_list],
        environment=env,
        illumination_fields=e_inc_list,
        wavelengths=[wavelength],
        device=struct_list.device,
        copy_structures=False,  # required: copy not allowed for autograd
    )
    sim.run(verbose=False, progress_bar=False)

    # --- calculate intensity at target position
    nf_target = sim.get_nf(
        wavelength=wavelength,
        r_probe=r_target,
        illumination_index=0,
        progress_bar=False,
    )
    I_center = nf_target["tot"].get_efield_intensity()  # field intensity

    return sim, I_center

run the optimization loop#

Note: For best convergence, reduce the learning rate and increase the number of iterations

t0 = time.time()
for i in range(OptConfig.n_iters + 1):
    optimizer.zero_grad()

    # --- evaluate fitness: maximize intensity at focal pos.
    sim, I_center = func(
        geo_pos,
        geo_rc,
        geo_rs,
        r_target,
        env,
        e_inc_list,
        wavelength=wavelengths[0],
        z0=z0_metasurface,
    )
    fitness = -1 * I_center

    # --- distance loss: don't overlapp geometries
    dist = torch.linalg.norm((geo_pos.unsqueeze(0) - geo_pos.unsqueeze(1)), dim=-1)
    dist = dist + torch.eye(len(dist), device=tg.device) * OptConfig.dist_min
    dist_clip = torch.clip(OptConfig.dist_min - dist, min=0)
    cummulated_dist = torch.sum(dist_clip)
    weighted_constraint = OptConfig.dist_weight * cummulated_dist

    # --- backpropagate gradients for total loss function
    loss = fitness + weighted_constraint
    loss.backward()
    optimizer.step()

    rad_core_nm = 50.0 + 80.0 * sigmoid(geo_rc / 200.0)
    rad_shell_nm = rad_core_nm + 30.0 * sigmoid(geo_rs / 200.0)

    # --- status printing every 5 iterations
    if i % 5 == 0:
        print(
            "iter #{} (time: {:.1f}s): loss = {:.2f}    (|E_focus|^2 = {:.1f}; distance constraint = {:.1f})".format(
                i,
                time.time() - t0,
                loss.squeeze().detach().numpy(),
                -1 * fitness.squeeze().detach().numpy(),
                weighted_constraint.squeeze().detach().numpy(),
            )
        )


print(
    "Final intensity enhancement |E_focus|^2 = {:.2f}".format(
        I_center.squeeze().detach().numpy()
    )
)

/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/torchgdm/tools/interp.py:87: UserWarning: Using a non-tuple sequence for multidimensional indexing is deprecated and will be changed in pytorch 2.9; use x[tuple(seq)] instead of x[seq]. In pytorch 2.9 this will be interpreted as tensor index, x[torch.tensor(seq)], which will result either in an error or a different result (Triggered internally at /pytorch/torch/csrc/autograd/python_variable_indexing.cpp:345.)
  numerator += self.values[as_s] * torch.prod(torch.stack(bs_s), dim=0)
iter #0 (time: 2.6s): loss = -0.82    (|E_focus|^2 = 0.8; distance constraint = 0.0)
iter #5 (time: 16.1s): loss = -3.78    (|E_focus|^2 = 3.8; distance constraint = 0.0)
iter #10 (time: 29.8s): loss = -7.66    (|E_focus|^2 = 7.7; distance constraint = 0.0)
iter #15 (time: 43.0s): loss = -10.18    (|E_focus|^2 = 10.2; distance constraint = 0.0)
iter #20 (time: 56.7s): loss = -11.05    (|E_focus|^2 = 12.0; distance constraint = 0.9)
iter #25 (time: 70.1s): loss = -13.02    (|E_focus|^2 = 13.0; distance constraint = 0.0)
iter #30 (time: 83.6s): loss = -13.54    (|E_focus|^2 = 13.7; distance constraint = 0.2)
Final intensity enhancement |E_focus|^2 = 13.71

plot the results#

# --- calc NF maps
r_probe_xy = tg.tools.geometry.coordinate_map_2d_square(D_area, n=121, r3=z_focus)
nf_res_xy = tg.postproc.fields.nf(sim, wavelengths[0], r_probe=r_probe_xy)

r_probe_xz = tg.tools.geometry.coordinate_map_2d(
    [-D_area, D_area], [-0.25 * z_focus, 1.5 * z_focus], 51, 151, r3=0, projection="xz"
)
nf_res_xz = tg.postproc.fields.nf(sim, wavelengths[0], r_probe=r_probe_xz)


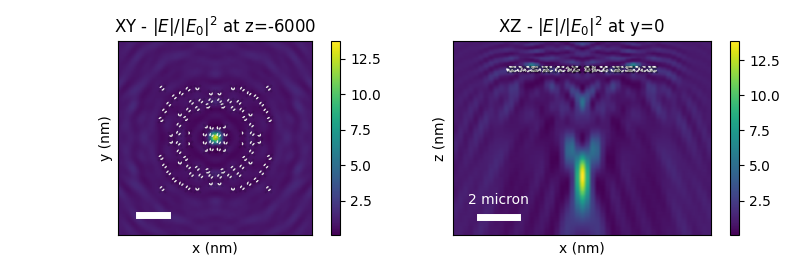
# --- plot nearfield intensity maps
plt.figure(figsize=(8, 2.7))

# - XY view
plt.subplot(121, title=f"XY - $|E|/|E_0|^2$ at z={z_focus}")
im = tg.visu.visu2d.field_intensity(nf_res_xy["tot"], rasterized=True)
plt.colorbar(im)
tg.visu2d.structure(sim, projection="xy", alpha=0.1, color="w", legend=False)
plt.plot([-5500, -3500], [-5500, -5500], "w-", lw=5)
plt.xticks([])
plt.yticks([])

# - XZ view
plt.subplot(122, title=f"XZ - $|E|/|E_0|^2$ at y=0")
im = tg.visu.visu2d.field_intensity(nf_res_xz["tot"], rasterized=True)
plt.colorbar(im)
tg.visu2d.structure(sim, projection="xz", alpha=0.1, color="w", legend=False)

plt.text(-4500, -7300, "2 micron", color="w", ha="center")
plt.plot([-5500, -3500], [-8000, -8000], "w-", lw=5)
plt.xticks([])
plt.yticks([])


plt.tight_layout()
plt.show()


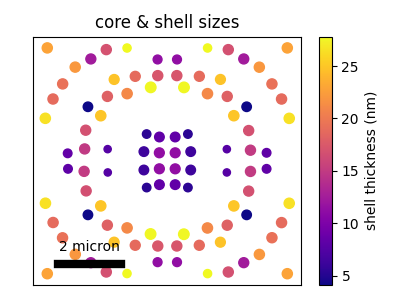
# --- plot structure
plt.figure(figsize=(4, 3))
plt.subplot(title="core & shell sizes", aspect="equal")
im = plt.scatter(
    *tg.to_np(geo_pos).T,
    s=tg.to_np(rad_core_nm) / 2,
    c=tg.to_np(rad_shell_nm - rad_core_nm),
    cmap="plasma",
)
plt.colorbar(im, label="shell thickness (nm)")

plt.text(-2500, -2900, "2 micron", ha="center")
plt.plot([-3500, -1500], [-3300, -3300], "k-", lw=6)

plt.xticks([])
plt.yticks([])

plt.tight_layout()
plt.show()

  0%|          | 0/15 [00:00<?, ?it/s]
batched nearfield calculation:   0%|          | 0/15 [00:00<?, ?it/s]
batched nearfield calculation: 100%|██████████| 15/15 [00:01<00:00, 12.92it/s]

  0%|          | 0/8 [00:00<?, ?it/s]
batched nearfield calculation:   0%|          | 0/8 [00:00<?, ?it/s]
batched nearfield calculation: 100%|██████████| 8/8 [00:00<00:00, 15.68it/s]

Total running time of the script: (1 minutes 27.433 seconds)

Estimated memory usage: 2951 MB

Gallery generated by Sphinx-Gallery

PyMieDiff + TorchGDM: Optimize a Huygens lens

Contents